수학
-

-
-
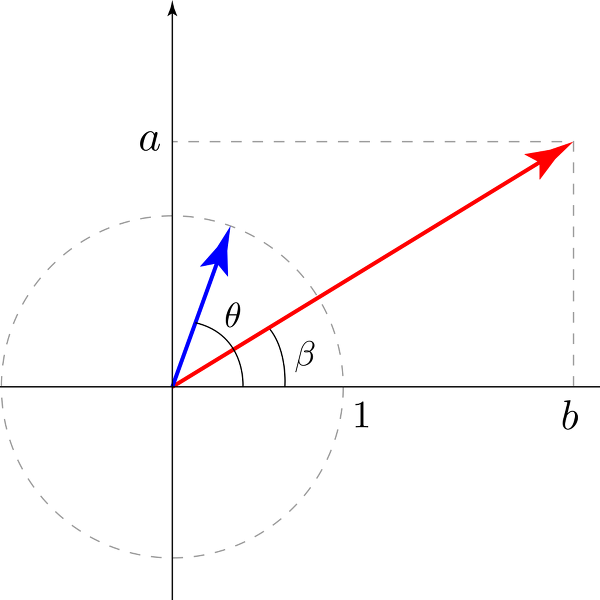
-
-

음악
-
-