먼저, 이 글을 작성하기 앞서, 이러한 흥미로운 주제에 대해 탐구할 수 있도록 해주신 수학 선생님께 감사의 인사를 드립니다.
미분가능하다는 것과 도함수가 연속이라는 조건이 서로 필요충분조건일까? 만약 아니다면, 서로의 포함관계가 있을까? 고등학교 과정에서는 대부분의 함수가 미분가능하면 그것의 도함수가 연속이기에 그렇게 걱정할 필요는 없지만, 그래도
수학적 호기심을 채우기 위해 탐구해보자.
사실 답부터 말하자면, 미분가능이라고 도함수가 연속인 것은 아니다. 하지만 그 역은 맞다. 이는 어찌보면 당연하다고 느낄 수 있는데, 많은 사람들이 간과하고 넘어가는 사실이다. 우리는 일상생활에서 너무나도 미분가능이라는 말이 도함수가 연속이라는 말과 동치라고 생각하고 살아가고 있는데, 그 단적인 예로 다음과 같은 구간별로 정의된 함수가 등장하였을 때다.
f(x)={f1(x)(0≤x<1)f2(x)(1≤x<2)
식 (1)
여기서 함수 f(x)가 x=1에서 미분가능하다고 문제가 주어졌을 때, 우리는 자연스럽게 f1(1)=f2(1)인지를 확인하고, f′1(1)=f′2(1)인지를 확인한다. 물론, 연속성을 확인할 때에도, 좌극한과 우극한으로 해야 하는 것이 맞지만, 더 큰 문제는 f(x)가 x=1에서 미분가능하다는 조건을 우리는 한 번도 f′1(1)=f′2(1)와 같은 일종의 도함수가 연속이라는 명제로 배운적이 없었다. 즉, 우리는 이미 머릿속에 있는 잘못된 개념으로 문제를 푸는 것이 습관화 되어있다는 것이다.
그러면, 진짜 이렇게 풀면 안되는 것일까? 솔직히 말하자면, 틀린 것은 맞지만, 그렇다고 답이 틀리다는 것은 아니다. 그러니까 사실 된다. 대부분의 함수에서는 된다. 그렇지만, 이것이 되는 이유와 그렇지 않은 함수를 알고 이렇게 푸는 것과 그렇지 않고 그냥 야매로 푸는 것은 크나큰 차이가 있다. 이에 대해 생각해 보기 위해 여러 특수함수들을 먼저 살펴보자.
1. sin1x
y=sinx의 그래프는 쉽게 그릴 수 있다. 그러나 다음과 같은 함수는 어떨까?
f(x)={sin1x(x≠0)0(x=0)
예측해보건대, x의 값이 줄어들면 줄어들 수록, sin내부의 값은 커지므로 원점 근방에서 무시무시하게 진동할 것 같다. x≥0인 구간에서 실제로 그래프를 그리면 다음과 같다.

일단, 이 함수는 원점에서 연속이 아니다. 그래서 그렇게 큰 의미는 없다. 당연히, 원점에서 미분도 불가능하다. 다른 함수를 알아보자.
2. xsin1x
그렇다면, 다음과 같은 함수의 그래프는 어떨까? f(x)={xsin1x(x≠0)0(x=0) 대충 생각하면, 임의의 실수 t에 대하여 −1≤sint≤1이므로, y=x와 y=−x에 접할 듯 싶다.
그래프는 다음과 같다.

이 함수는 큰 특징을 가지고 있다. 바로, 원점에서 연속이라는 것이다. 그도 그럴 것이, lim이기 때문이다. 그렇다면, 원점에서 과연 미분가능할까? 미분계수의 정의를 사용하여 알아보면,
f'(0) = \lim_{x \to 0} {\frac{f(x) - f(0)}{x}} = \lim_{x \to 0}\frac{x \sin \dfrac{1}{x}}{x} = \text{(발산)}
따라서, 원점에서 미분계수는 진동발산하므로, 이 함수는 원점에서 미분가능하지 않다.
그러면, 이를 확장하여 다른 함수도 알아보자.
3. x^2 \sin \dfrac{1}{x}
이번에는 앞에 곱해진 것이 이차다. 좀 더 정확히 쓰면, f(x) = \left\{\begin{array}{lr} x^2 \sin \dfrac{1}{x} & (x \ne 0)\\ 0 & (x=0) \end{array}\right. 이와 같은 함수이다. 이 또한 그래프를 추정해보면, y=x^2과 y=-x^2에 접하면서 유계 되어있을 것이다. 그래프를 살펴보자.

확실히 그래프가 Figure 2 보다는 매끄러운 모양이다. 여기서 매끄럽다는 것은 \sin함수 자체가 매끄럽다는 것이 아니라, 그 접하는 선, 증가나 감소하는 경향이 매끄럽다는 것이다. 그래서 뭔가 y=x \sin\frac{1}{x}와는 성질이 다를 것 같다.
연속성을 조사해보자. 자명하게, f(0) = \lim\limits_{x \to 0} f(x)이므로, 연속이다.
그렇다면, 중요한 미분가능성을 판단해보자. 미분계수의 정의를 사용하여 x=0에서의 미분계수를 구해보면,
f'(0) = \lim_{x \to 0} {\frac{f(x) - f(0)}{x}} = \lim_{x \to 0} \frac{x^2 \sin \dfrac{1}{x}}{x} = \lim_{x \to 0} {x \sin \dfrac{1}{x}} = 0 깔끔하게 f'(0)=0이 나온다. 즉, 원점에서 미분가능하고 그 값이 0이라는 것이다.
그런데, 그렇다면 정말로 해보고 싶었던 것. 과연 도함수는 연속인가? 도함수는 쉽게 구할 수 있다. 곱의 미분을 사용하면, f'(x) = 2x \sin \frac{1}{x} - \cos \frac{1}{x} \quad (x \ne 0) 그렇다면, 이 구한 도함수의 연속성을 파악해보자.
\begin{array}{c} \lim\limits_{x \to 0-} f'(x) = \lim\limits_{x \to 0-} \left( 2x \sin \dfrac{1}{x} - \cos \dfrac{1}{x}\right) = \text{(발산)}\\ \lim\limits_{x \to 0+} f'(x) = \lim\limits_{x \to 0+} \left( 2x \sin \dfrac{1}{x} - \cos \dfrac{1}{x}\right) = \text{(발산)} \end{array}
따라서, 애초에 f'(x)의 x=0에서의 극한값이 발산하므로, 당연히 0=f'(0)\ne \lim\limits_{x \to 0} f'(x)이고 그러므로 도함수는 연속이 아니다.
신기하지 않은가? 미분가능한데, 도함수는 연속이 아니다. 결론적으로, 이러한 함수가 존재하기 때문에 우리는 미분가능성을 판단하는 문제를 도함수의 연속 여부로 해석하면 안된다.
도함수의 불연속성
이렇게, 우리는 특이한 함수를 관찰하며 미분가능이지만 도함수가 연속이 아닌 예시를 찾아봤다. 그런데, 이쯤 들면 드는 생각 한 가지가 있다. 앞서 봤던 예시는 도함수가 불연속이지만, 좌극한과 우극한이 모두 발산하며 불연속인 경우였다. 하지만, 우리는 함수의 불연속이라는 이미지를 떠올렸을 때, 좌극한과 우극한, 그리고 함숫값이 서로 다른 유한한 값으로 수렴하는 경우도 떠올린다. 즉, 다음과 같은 경우이다.
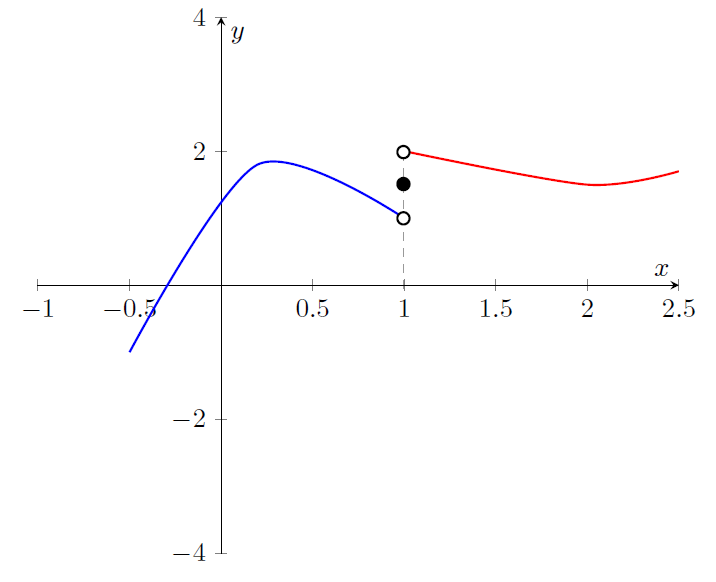
Figure 4와 같은 경우는 x=1에서 불연속인데, 함숫값은 3/2이고 좌극한은 1로, 우극한은 2로 수렴하는 경우이다. 즉, 이렇게 좌극한과 우극한이 유한한 값으로 수렴하는 경우도 불연속이다. 그렇다면, 과연 도함수가 이렇게 불연속이 될 수 있을까?
어떤 사람은 가능하다면서, 도함수가 가우스 함수(계단 함수)인 예시를 든다. 그런데, 이러한 계단 함수는 정적분은 가능하지만, 그것의 부정적분은 알 수 없다. 따라서 이러한 예시는 옳지 않다.
그렇다면, 진짜로 도함수의 좌극한과 우극한이 유한한 값으로 수렴하면서 불연속일 수가 있을까? 결론부터 말하자면 불가능하다. 충분히 증명할 수 있다.
한 번, 증명을 보기 전에 스스로 해보길 바란다. 힌트는 평균값 정리이다.
x=a를 포함하는 구간 I에서 정의된 함수 f(x)에 대하여 x=a에서의 미분계수를 f'(a)라고 하자. 그리고 f(x)의 도함수를 f'(x)라 하고, 좌극한값 \alpha와 우극한값 \beta를 다음과 같이 정의하자. \begin{array}{c} \alpha := \lim\limits_{x \to a-} f'(x) \\ \beta := \lim\limits_{x \to a+} f'(x) \end{array} 함수 f(x)가 x=a에서 미분가능하고, 따라서 f'(a)는 미분계수의 정의에 따라 다음과 같이 나타낼 수 있다. \begin{array}{lr} f'(a) & = \lim\limits_{x \to a-} \dfrac{f(x) - f(a)}{x-a} \\\\ & = \lim\limits_{x \to a+} \dfrac{f(x) - f(a)}{x-a} \\ \end{array} f는 [x,a]에서 연속이고, (x,a)에서 미분 가능하므로, 평균값 정리에 따라 \dfrac{f(x) - f(a)}{x-a} = f'(c_x)인 c_x가 구간 (x,a) 내에 존재한다. 따라서 여기에 좌극한을 취해주면, x \to a- 일 때 c_x \to a-이므로, f'(a) = \lim\limits_{x \to a-} \dfrac{f(x) - f(a)}{x-a} = \lim_{c_x \to a-} f'(c_x) = \alpha 그러므로, f'(a) = \alpha = \lim\limits_{x \to a-} f'(x)이다.
그리고, 마찬가지로 f는 [a,x]에서 연속이고 (a,x)에서 미분 가능하므로 평균값 정리에 따라 \dfrac{f(x) - f(a)}{x-a} = f'(d_x)인 d_x가 구간 (a,x) 내에 존재한다.
여기에 우극한을 취해주면 x \to a+ 일 때 d_x \to a+이므로, f'(a) = \lim\limits_{x \to a+} \dfrac{f(x) - f(a)}{x-a} = \lim_{d_x \to a+} f'(d_x) = \beta 따라서 결론적으로 f'(a) = \alpha = \beta 이다.
이는 우리에게 식 (1) 과 같은 문제가 주어졌을 때, 식 (1) 함수의 도함수가 연속이면 미분가능하다는 명제를 도함수가 연속이라는 명제로 해석해도 문제가 없다는 것을 함의한다.
'수학📐' 카테고리의 다른 글
| 표본(+표본평균, 표본분산)에 관하여 (0) | 2020.07.27 |
|---|---|
| #2 (1) | 2020.04.20 |
| 각의 이등분선의 방정식 (1) | 2020.04.20 |
| 특수한 분수함수의 극대, 극소 (0) | 2020.03.08 |
| #1 (0) | 2020.02.27 |


